A diferencia de la publicación anterior, que apelaba a la estadística descriptiva para comparar entre sí las situaciones de las jurisdicciones de nuestro país más castigadas por esta pandemia, esta quinta entrega pretende contribuir al entendimiento de la dinámica de la misma desde el punto de vista epidemiológico. Debido a ello, probablemente generará mayor interés en aquellas personas con conocimientos previos sobre esta ciencia, sobre todo si además cuentan con cierta formación en matemáticas y estadística inferencial.
Deseo destacar que una buena parte del texto aquí presentado no es de mi autoría, sino que reproduce en forma parcial o resume informes científicos originales, aparecidos en diferentes publicaciones. Quedo a disposición de quien lo desee para hacerle llegar copias de (o links a) los mismos.
BREVE HISTORIA Y CONCEPTOS BÁSICOS SOBRE EPIDEMIOLOGÍA
Las epidemias acompañan a la humanidad desde tiempos remotos: a modo de ejemplo, las llamadas “plagas de Egipto” y la viruela aparecieron hace miles de años. Luego del comienzo de la era cristiana ocurrieron pandemias que causaron tremendos efectos sobre la población mundial, y varias de ellas generaron la muerte de millones de personas, como fue el caso de la peste negra o peste bubónica (75 millones), la gripe española (entre 50 y 100 millones), el sarampión (200 millones) y la viruela en sus diferentes oleadas (300 millones), solo por citar las más importantes.
Estas enfermedades fueron impulsando el desarrollo de estudios epidemiológicos por parte de científicos en todo el mundo y también, la aparición de las primeras vacunas, algunas de las cuales fueron tan exitosas que llegaron a prácticamente eliminar algunas muy letales, como fueron los casos de la poliomielitis, el sarampión y en especial, la viruela, cuya letalidad llegó a ser del 30 % y ya hace varias décadas fue declarada como erradicada, pues el último caso oficialmente confirmado data del año 1977.
Entre dichos estudios se destaca el elaborado por los matemáticos Kermack y McKendrick, publicado por la Sociedad Real de Ciencias Matemáticas y Físicas en el año 1927 en Inglaterra, bajo el título “Una Contribución a la Teoría Matemática de las Epidemias”.
Estos autores desarrollaron un modelo epidemiológico compartimentado básico, al que denominaron “Modelo SIR”, a modo de sigla de las palabras Susceptible–Infectado–Recuperado, en el que S, I, y R representan los tres compartimientos. En este relativamente sencillo modelo, ideado para describir epidemias, todos los individuos son categorizados al comienzo como potencialmente susceptibles a un agente patógeno determinado y, si se infectan, van pasando a los otros dos compartimientos. Incluye algunos parámetros e hipótesis previas, entre ellas las siguientes:
- Se considera que todos los integrantes de la población presentan el mismo grado de probabilidad de contraer la enfermedad.
- La cantidad de integrantes de la población se mantiene estable en el tiempo, pues no entra ni sale nadie de la misma, y la tasa de nacimientos es igual a la de fallecimientos.
- No se dispone de vacuna, por lo menos en las primeras etapas de la epidemia.
Al momento de producirse el primer caso (el actualmente llamado “Caso 0”), el infectado pasa desde el compartimiento S (Susceptible) al I (Infectado). Como este individuo está en contacto con el resto de la población y la enfermedad es contagiosa, comienzan a aparecer más infectados, que también pasan de S a I. Los que integran el grupo I tienen tres alternativas en el tiempo, dependiendo de las características de la enfermedad y de la capacidad de asistencia médica disponible: o continúan infectados – con lo cual, siguen siendo “contagiantes” y permanecen en el grupo I –, o fallecen, o se recuperan, pasando al compartimiento R. Mientras eso ocurre, los no contagiados continúan formando parte del grupo S. Respecto a los R, surge aquí un aspecto clave, cual es la adquisición o no de inmunidad por parte de los R: si un R no la adquiere, vuelve al grupo S (como es el caso de la gripe común); si ya queda inmune, como ocurre por ejemplo con la paperas, el grupo S queda cada vez con menos miembros, y el grupo R cada vez es más numeroso. Esto último es lo que se espera que ocurra con la enfermedad Covid-19, aunque no está todavía confirmado. Si bien los autores no lo mencionan, obviamente los fallecidos se pueden agregar a un cuarto grupo: los F (Fallecidos).
De más está decir que la aparición de vacunas eficaces es de enorme importancia, pues evita el pasaje de R a S o, dicho de otro modo, genera el pasaje inmediato del grupo S al grupo R (al cual, dado esto, podríamos renombrar como Resistentes), sin pasar por el compartimiento I.
Expresando esto en Matemáticas simplificada, si llamamos So a la población inicial, y Si a esa misma población, en un dado momento que llamaremos i, la cantidad de integrantes del grupo Si viene dada por la siguiente ecuación:
(1) Si = So – Ii – Ri – Fi
Se podría suponer que la no definición por parte de los autores del grupo F – y por lo tanto, su no inclusión en las ecuaciones matemáticas – se debió a que, en general, el mismo es cuantitativamente despreciable en relación al grupo S: en el caso concreto de Covid-19, y si bien es la primera – y para muchos probablemente la única – pandemia que nos tocará vivir durante nuestra existencia (y por eso, tanto nos impacta), la cantidad de integrantes del grupo F es muy baja en relación a la de los integrantes del grupo S: tomando los datos actuales a nivel mundial, 1 de cada 300 personas está o estuvo infectada, y 1 de cada 30 infectados falleció, con lo cual hasta ahora 1 de cada 9.000 personas ha fallecido debido a la enfermedad Covid-19 en todo el mundo. En el caso de Argentina, estos números son respectivamente de alrededor de 1/100, 1/50 y 1/5.000.
Dado que en las etapas iniciales de una epidemia, la cantidad de integrantes del grupo I es mucho menor que la del grupo S, la lógica indica que es a los del grupo I a los que hay que aislar para proteger a los del grupo S, y no al revés. Sin embargo, como al comienzo es difícil identificar a los I y, a diferencia del modelo planteado por Kermack y McKendrick, existe o puede existir el riesgo de ingreso de infectados externos a la población total (cosa que ocurrió en todos los países, incluyendo el nuestro), el aislamiento inicial de los S parece una medida razonable, a fines de que el país se prepare desde lo sanitario y a la vez, concentre sus esfuerzos en controlar y aislar en forma preventiva a los ingresantes. Sin embargo, y luego de que se haya logrado cesar dichos ingresos, la situación cambia, como veremos más adelante.
El trabajo de Kermack y McKendrick fue retomado recién a fines de la década de 1970 por los investigadores Anderson y May, quienes lo aplicaron para estudiar estrategias de control de enfermedades infecciosas en su trabajo “Biología de Población de Enfermedades Infecciosas”, publicado en la Revista Nature en 1979.
R0 O NÚMERO REPRODUCTIVO BÁSICO
Siguiendo ahora a Anderson y May en cuanto a la dinámica, el ritmo de pasaje desde un compartimiento a otro va a depender de los siguientes parámetros, todos referidos a la misma unidad de tiempo y a la población S:
- Tasa de transmisión Tt, o “contagiosidad”
- Tasa de recuperación Tr
- Tasa de mortalidad Tf
Fácilmente se puede deducir que si la Tasa de transmisión Tt es mayor que la Tasa de recuperación Tr, la enfermedad va a difundirse cada vez a mayor ritmo; si son iguales, la enfermedad seguirá difundiéndose a ritmo constante, y si Tt es menor a Tr comenzará a reducirse, hasta eventualmente desaparecer.
La relación entre Tt y Tr es conocida como “Número Reproductivo Básico” o R0:
(2) R0 = Tt/Tr
Este número es también interpretado como la cantidad de personas que contagia cada infectado, en la etapa infectiva de cursado de la enfermedad la que, para Covid-19, ha sido estimada en 4-5 días, pues es el período asintomático (también llamado “de latencia” o “prodrómico”), aunque este período puede ser mayor si no se aísla al enfermo. Sin embargo, la interpretación mencionada no es estrictamente cierta, como veremos en el siguiente punto.
Re O NÚMERO REPRODUCTIVO EFECTIVO
Obviamente, Si no puede ser mayor que So, y además, tiende a ser cada vez menor, a medida que se desarrolla la epidemia. Esto ocurre porque, siguiendo la ecuación (1), van aumentando los I, los R y – en caso de ya existir la vacuna – los de un subgrupo del grupo R: los del grupo V (Vacunados), en detrimento de los S.
Con el paso del tiempo – y siempre que los R no regresen al estado S –, la menor presencia de integrantes del grupo S necesariamente generará una disminución en la tasa de infección, pues el virus no encontrará a quién infectar o, dicho de otro modo, las posibilidades de encuentro entre una persona infectiva y una susceptible serán cada vez menores. Este es la idea en la cual se fundamenta la actualmente llamada “inmunidad colectiva” o “inmunidad de rebaño”, que cuenta tanto con defensores como con detractores.
De la cuantificación de los integrantes de cada compartimiento o grupo y el procesamiento estadístico de los datos reales generados por la epidemia, surge un nuevo concepto: el Re, o Número Reproductivo Efectivo, que viene dado por la siguiente fórmula:
(3) Re = R0 x (Si/So)
A mi modesto juicio, es el Re el número que debe utilizarse, y no el R0, pues este último no contempla la disminución en el tiempo de la población del grupo S (Si) en relación a la población total inicial (So), cosa que sí ocurre con Re: nótese que, para un mismo R0, cuanto menor sea el cociente Si/So, menor será el valor de Re, lo que es lógico pues – si los R adquieren inmunidad – quedará cada vez menos gente susceptible a enfermarse.
Por otro lado cabe señalar que si R0 representa la cantidad de personas que pueden ser contagiadas por cada enfermo durante su período infectivo, pequeñas variaciones de R0 generan enormes variaciones en la cantidad de infectados: a modo de ejemplo, Si R0 es igual a 1,1, en veinte semanas tendríamos 7 contagiados por cada infectado inicial, pero si R0 es igual a 1,5 tendríamos 3.325 contagiados, y si es igual a 2, ese número sería superior a 1.000.000 de personas.
En resumen, mi opinión es que el número que se menciona como R0 – especialmente en la Ciudad de Buenos Aires – es en realidad el Re.
MODELOS MÁS COMPLEJOS Y EL R0
El modelo básico SIR explicado más arriba puede someterse a muchas mejoras: en ese modelo se parte del supuesto de que todos los individuos pertenecen a una gran población “panmíctica” (es decir, “bien mezclada”), en la que todos tienen las mismas probabilidades de entrar en contacto entre sí. Por lo común, este supuesto no es lógico para la mayor parte de las poblaciones humanas, que con frecuencia están estructuradas en subgrupos cuyos individuos tienen más probabilidades de relacionarse entre sí, que con los individuos de otros subgrupos. Por tal motivo, los modelos epidemiológicos suelen basarse en poblaciones estructuradas por edad. Esos modelos requieren ecuaciones semejantes a la ecuación (1), pero para cada grupo de edad, que describan la transmisión de la enfermedad dentro de ese grupo y entre otros grupos etarios. Otro método común para incorporar la estructura de la población consiste en incluir en el modelo variables como familia, lugar de trabajo, escuela y grupos comunitarios.
Muchos modelos pueden incorporar también una estructura de “metapoblación” (una serie de poblaciones conectadas) para describir la dinámica de la enfermedad en muchas ciudades. En estos modelos, la dinámica en la metapoblación explica la propagación de la enfermedad de una ciudad a otra.
También es frecuente agregar factores demográficos a los modelos compartimentados, para que estos sean más realistas. Los factores de este tipo que se incluyen son nacimientos, defunciones, inmigración y emigración, que evidentemente ocurren en casi todas las poblaciones. Además de simular poblaciones más realistas, los especialistas en modelización pueden hacer más complejos estos modelos dinámicos. En particular, con frecuencia incluyen en los mismos intervenciones de salud pública, para poner a prueba el posible efecto de una o varias de estas. Los modelos compartimentados permiten incluir diversas intervenciones, como el uso de antivíricos, vacunas, mascarillas, lavado de manos, cierre de escuelas, distanciamiento social, aislamiento o cuarentena. Cada una de esas intervenciones requiere la adaptación de las ecuaciones, que a veces son muchas, para incorporar nuevos compartimentos y parámetros.
Vale la pena señalar que muchos modelos compartimentados también permiten incluir varias cepas del virus, ya que un agente patógeno puede tener muchas variantes genéticas (cepas) que circulan en la población. Los modelos mencionados se pueden modificar para incluir diversas cepas y las consecuencias emergentes, como la sinergia o la interferencia entre ellas. Prácticamente cualquiera de las modificaciones antedichas cambiará la dinámica pronosticada de la enfermedad.
Como se mostró líneas arriba en los modelos de enfermedad sencillos, la estimación del R0 no siempre permite hacer inferencias útiles. Al aumentar la complejidad, la estimación de todos los parámetros puede volverse agobiador. A menudo es difícil establecer firmemente los pocos parámetros que son decisivos en un modelo SIR. En la práctica, los valores de los parámetros proceden con frecuencia de un puñado de estudios cuya aplicabilidad tal vez no sea amplia.
Habida cuenta de la dificultad para medir simplemente los parámetros generales a nivel de la población de una enfermedad dada, parece poco probable que la edad, la población, las intervenciones o los parámetros pertinentes a una cepa en particular se puedan estimar con la rapidez suficiente para incorporarlos en la planificación de respuestas de salud pública específicas.
El aspecto sobresaliente es que hay métodos diferentes y cada uno puede arrojar una estimación distinta del R0. En consecuencia, el uso del número reproductivo básico para pronosticar la tasa de ataque depende del modelo empleado.
Después de considerar las cuestiones anteriores, se puede concluir que la estimación del número reproductivo básico (R0) de una epidemia de una enfermedad en particular tiene poca utilidad fuera del grupo de población del cual provienen los datos.
Se podría afirmar también que la estimación de las razones reproductivas puede aportar información útil durante las epidemias, en especial, el número de reproducción efectiva, pues cuantifica la propagación de una enfermedad contagiosa en una población. Como ya vimos, cuanto más altos son los valores, más rápida es la circulación del agente infectivo. La estimación de las razones reproductivas basadas en datos de una población en particular es útil sólo para esa población. En esencia, este parámetro es la tasa de crecimiento exponencial de una epidemia en curso y, por lo tanto, brinda información acerca de la tasa de transmisión en la población en estudio en un momento dado.
A fin de que las tasas de crecimiento basadas en valores específicos de R puedan usarse con fundamento para adoptar decisiones de salud pública, hay que resolver otras cuestiones tales como la obtención de los datos necesarios para establecer estimaciones uniformes con intervalos de confianza estrechos.
Si existieran mecanismos para estimar los valores de Re > 1 al instante o casi al instante, los funcionarios de salud pública podrían determinar si determinadas estrategias de intervención —como el cierre de las escuelas o la cuarentena— están modificando la dinámica de la enfermedad y si, por lo tanto, deben mantenerse. Resulta poco probable que la eficacia de una intervención en epidemias del pasado pueda aplicarse a una epidemia contemporánea, debido a los cambios de la estructura social, el medioambiente, los agentes patógenos, etc.
Es preciso reconocer que, aun cuando la capacidad de estimar los números reproductivos al instante pudiera ser ventajosa, la eficacia de una intervención determinada puede variar temporal y geográficamente debido a los cambios del ambiente, la estructura de la población, la evolución del virus y la inmunidad; por lo tanto, las estimaciones respecto de una región pueden no ser aplicables a otra.
La razón reproductiva básica de una epidemia es una propiedad compleja, que depende específicamente del modelo utilizado para calcularla, de la población en estudio (por lo que toca a las modalidades del contacto y las características demográficas), el huésped, el agente patógeno y, con frecuencia, la cepa específica de este. Así pues, aunque el R0 es una propiedad intuitiva de una epidemia, no resulta particularmente eficaz para determinar la posible utilidad de las medidas de control. Aun así, cuando se considera como parte de una serie de características estimadas de una epidemia, el R0 puede ser útil para tomar decisiones de salud pública. Aunque los especialistas en la elaboración de modelos de enfermedades infecciosas reconocen la importancia de las cuestiones hasta aquí expuestas, las personas que aplican los resultados de modelos matemáticos para organizar respuestas de salud pública a veces no conocen a fondo esos aspectos. Si las estimaciones del R0 se van a utilizar para determinar las respuestas de salud pública, los formuladores de políticas deben ser informados claramente de las limitaciones mencionadas. Además de destinar recursos para calcular el R0, hay que invertir en la estimación de otros parámetros epidémicos como las tasas de transmisión, los períodos infecciosos o los períodos de latencia, los cuales son más pertinentes para la respuesta de salud pública a los brotes de enfermedades infecciosas, en especial las pandemias de gripe.
APLICACIÓN DE UN SISTEMA DE CÁLCULO DE R0 y Re
A fines del mes de Agosto de 2020 pude acceder a un trabajo denominado “Estimación de los Números de Reproducción Básico (R0) y Efectivo (Re) – Propuesta para su Medición y Seguimiento Pandemia COVID-19 – Departamento Tarija”, publicado por el MSc. Dr. Carlos Adolfo Barrero Ortega, Medico Salubrista y Epidemiólogo y Consultor Nacional en Salud en la hermana República de Bolivia.
Luego de tomar contacto con él, gentilmente me facilitó el acceso a un software denominado EpiEstim, desarrollado por el Departamento de Epidemiología de Enfermedades Infecciosas del Imperial College (Londres, Reino Unido) y puesto a disposición pública por la OMS y la OPS.
En su trabajo, el Dr. Barrero afirma que “el Número Reproductivo Efectivo (Re) es posiblemente el indicador más importante para caracterizar la dinámica de la pandemia COVID-19 y evaluar el efecto de las intervenciones que se planificaron y ejecutaron como política de mitigación de contagios en la población susceptible”.
Una de las principales limitaciones para conocer su valor preciso es la falta de certeza respecto a la cantidad real de personas infectadas en cada período de tiempo: a nivel mundial, se estima que es o fue muy superior a la registrada en cada país, región o localidad. Esta situación genera en forma directa una correlativa subestimación de la tasa de incidencia de la enfermedad (es decir, del valor Tt, que como ya dijimos, es la relación numérica entre la cantidad de personas infectadas y el total de la población en un determinado período de tiempo). Si esto ocurre, y dado que la tasa de recuperación (Tr) suele ser más exactamente conocida, el cociente R0 termina siendo subvaluado.
De la experiencia recabada en otros países y/o grandes ciudades afectadas por Covid-19, el R0 tiende a aproximarse al valor 1 cuando la tasa de incidencia real de la enfermedad es de entre el 10 y el 20 % del total de la población. Si tomamos por caso a la CABA – el distrito con mayor tasa de incidencia en la Argentina – y ateniéndonos a los casos oficialmente confirmados, ese porcentaje es actualmente del orden del 1,85 %, todavía muy bajo respecto a los anteriormente citados. Esto lamentablemente indicaría que estamos recién en las etapas iniciales de la evolución de esta enfermedad en todo el país.
Como elemento a favor y en relación a la baja tasa de letalidad de la enfermedad en nuestro país (apenas superior al 2 %), algunos investigadores opinan que la cepa viral circulante en Argentina es distinta y menos letal que la que generó las altas mortalidades registradas en Europa y parte de Asia.
Volviendo al EpiEstim, el mismo toma una serie de datos y parámetros previos, cuya complejidad excede los límites del presente escrito. Sólo mencionaré sus principales datos de entrada, que son los siguientes:
- Incidencia: Es la cantidad de nuevos casos informados para cada serie de tiempo.
- Serie de tiempo: Se establece en forma previa. Para epidemias de corta duración o para sus etapas iniciales, se suelen cargar datos diarios.
- Longitud de cada período de análisis: Equivale a la cantidad de días (semanas, o meses) al que el usuario le pide al sistema que realice cada cómputo. El más usado en Argentina en la presente pandemia es de 7 (siete) días.
RESULTADOS PARA ARGENTINA – PERÍODO 03/03/2020 AL 31/08/2020
El siguiente cuadro presenta los resultados numéricos obtenidos para todo el país desde la aparición del primer caso, el 03/03/2020. La curva en verde corresponde a los datos diarios; la curva en rojo continuo al valor Re, y las curvas en rojo discontinuo muestran el llamado “intervalo de confianza”, con una probabilidad de 0,95. En forma simplificada podría decirse que lo que marcan las mismas son los valores extremos máximos y mínimos entre los que se ubica el valor medio real de Re (estrictamente, la mediana), con una probabilidad del 95 %. La línea azul, finalmente, muestra el valor umbral de 1, cuyo significado ya explicamos al inicio del presente escrito.
Como se puede observar, la casuística o incidencia diaria presenta una clara tendencia ascendente. En cuanto al Re y dejando de lado los primeros valores, que por lo temprano de la infección resultan exageradamente elevados, se puede ver que en ningún momento estuvo por debajo de 1, aún cuando resultó prácticamente igual a ese valor en tres ocasiones, que corresponden respectivamente a los días 13/04, 03/05 y 25/08. Al 31/08 se ubicaba en un preocupante 1,35 como promedio nacional, con un gran peso relativo de la Provincia de Buenos Aires y en especial, del conurbano bonaerense.
RESULTADOS PARA TUCUMÁN – PERÍODO 01/06/2020 AL 31/08/2020
Haciendo correr el sistema de cálculo para nuestra Provincia, surge el siguiente gráfico:
Con valores iniciales erráticos, debidos a la baja cantidad de casos, el número Re tiene un importante pico entre los días 55 y 65 de la serie, entre fines de Julio y comienzos de Agosto, consecuencia de un importante incremento en los casos diarios promedio de 7 días. Finalmente, hacia fines de Agosto el Re tiende a estabilizarse, pero a un nivel tan elevado como 2,3.
RESULTADOS PROVINCIA DE BUENOS AIRES, CABA Y CHACO – 01/06/2020 AL 31/08/2020
En los siguientes gráficos presento la evolución de la Incidencia y del Número de Reproducción Efectivo Re para estos, importantes por su cantidad de habitantes y también por su alto nivel de contagios.
Salvo un corto período de 2-3 días, el Re de Provincia de Buenos Aires fue siempre para el lado de la expansión de los casos, y actualmente está largamente por arriba del número “umbral” de 1. Cabe señalar también que estos son los datos a nivel provincial (casi 16 millones de personas); aplicando esta misma fórmula sólo al llamado “Gran Buenos Aires” seguramente el valor sería claramente mayor.
Distinta es la situación de la Ciudad de Buenos Aires, la que con sus poco más de 3 millones de habitantes se mantiene desde hace varias semanas en valores de incidencia diaria casi constantes, lo que se refleja en un Re oscilante alrededor del valor neutro. Si bien esto es comparativamente bueno, mientras el Re no baje seguirá habiendo día tras día una alta cantidad de nuevos infectados a quienes atender.
Algo similar a la CABA ocurre en Chaco, como se puede ver en el siguiente gráfico:
Aunque felizmente los casos positivos registrados son muy estables a lo largo de los días, lo notorio es que el Re no desciende por debajo de 1, lo que implica que los contagios continúan ocurriendo, aunque con una baja tasa de contagiosidad (prácticamente 1 a 1).
RESULTADOS PARA OTRAS JURISDICCIONES
En los siguientes gráficos presento la evolución de la Incidencia y del Número de Reproducción Efectivo Re para los restantes cuatro distritos con más casos positivos:
Puede verse que Jujuy y Córdoba están en una clara situación de expansión de la enfermedad, especialmente Córdoba la que además, tiene más población y por lo tanto, como ya vimos, hay más personas susceptibles de contraer la enfermedad.
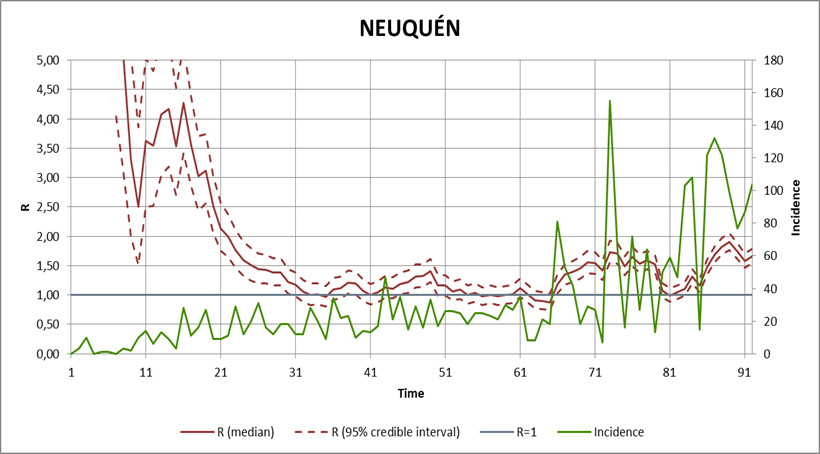
Por último presento los datos de Neuquén y Río Negro. Estas dos provincias patagónicas son vecinas y además, sus principales focos de contagio están “pegados” entre sí (Neuquén Capital en la provincia homónima, y Cipoletti y General Roca en Río Negro). Al respecto recuerdo la inevitable interacción entre poblaciones que mencioné al comienzo, que también se da en otras jurisdicciones, como es el caso de CABA y el Gran Buenos Aires, y más aquí, San Miguel de Tucumán y las ciudades limítrofes (Alderetes, Las Talitas, Banda del Río Salí, etc.). Probablemente sus curvas de Re tiendan a tener con el tiempo un comportamiento similar. Por ahora se las ve bastante “inquietas”, como ocurre con la de Tucumán.
CONCLUSIONES
Si bien los Números Reproductivos R0 y Re son sólo aproximaciones a la realidad, lo que muestran es que la Argentina está en en una etapa inicial de avance de esta epidemia, y que además, el virus se está diseminando en provincias y regiones que venían estando bastante preservadas hasta ahora.
Este fenómeno es similar al que ocurrió por ejemplo en USA, donde migró desde la costa Este hacia la costa Oeste y hacia el Sur, o en Italia, donde comenzó en la Lombardía (en el Norte), para luego irse trasladando hasta llegar a Campania y Sicilia (en el Sur).
Un aspecto preocupante es que en general, el Norte de Argentina dispone de mucho menos recursos sanitarios que la zona central, y existen allí centros poblados de alta densidad demográfica, como es particularmente el caso de Tucumán.
Por otro lado y tal como intenté explicar en anteriores artículos, no es de esperar que la curva de reducción muestre una mayor tasa de variación que la de propagación: siguiendo la curva logística ya descripta, aún cuando el Re pase a valores menores a 1, tenemos un largo tiempo por delante de convivencia con la enfermedad Covid-19 (por lo menos igual al ya transcurrido), mientras no aparezca una vacuna efectiva que se aplique a la mayor parte o a toda la población de nuestro país.
Como aspecto positivo, las relativamente bajas tasas de letalidad y/o la severidad de la enfermedad causada por el virus circulante podría indicar que la carga viral aquí es menor, o que se trata de una cepa más “benigna” en cuanto a sus efectos sobre las personas infectadas.
Para finalizar, resulta obvia la necesidad de reforzar la adecuación del comportamiento social a esta amenaza, aspecto este que no depende sólo del accionar de las autoridades de gobierno o de los agentes sanitarios, sino del de la población en su conjunto.